
Two facts contribute to the slippery quality of prime numbers, that there are so many and they do not occur in any particular order. This fact leads to an obvious question -how can all the prime numbers be located? The answer is simple - they cannot, at least not yet. Although this may seem odd, the fact remains that the supply of prime numbers is unlimited. This contradicts the original assumption, proving that there really are an infinite number of primes. The number produced will not be divisible by any prime number evenly (there will always be a remainder of 1), which indicates primacy.
Prime numbers plus#
That means that X is equal to the product of all the primes plus 1. Now, form the equation p 1p 2p 3.p N + 1 = X. Assume all prime numbers can be listed like this: p 1, p 2, p 3.p N, with p 1 =2,p 2 =3, p 3 = 5, and p N = the largest of the prime numbers (remember, we are assuming there are a finite, or limited, number of primes). All facts in mathematics must be backed by a proof, and this one is no exception. Finding prime numbersĪny discussion on the location process for prime numbers must begin with the statement of one fact: there is an infinite number of prime numbers. Since then, prime numbers have proved to be elusive mysteries in the world of mathematics. Mathematicians began putting forth ideas concerning prime numbers as early as 400 BC, but Greek mathematician Euclid is largely credited with publishing the first concrete theories involving prime numbers in his work Elements (c.
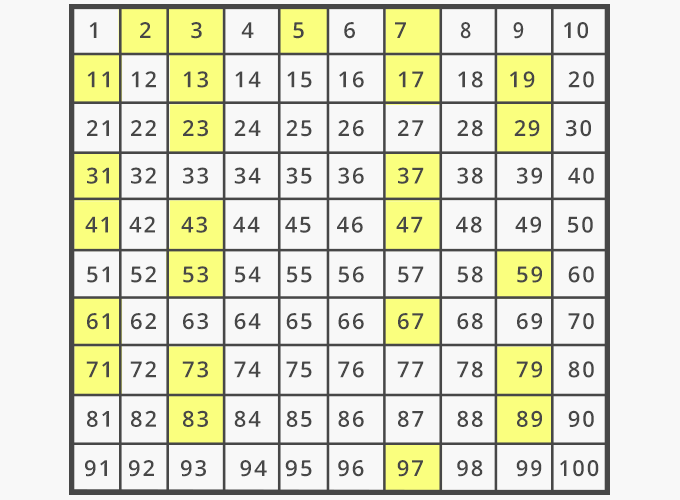

The idea of primacy dates back hundreds of years. The only even prime number is 2, since all other even numbers are at least divisible by themselves, 1, and 2. A prime number is any number greater than 1 that is divisible only by itself and 1.


 0 kommentar(er)
0 kommentar(er)
